Integration By Substitution - Geneseo Math 222 01 Inverse Trig Functions / In this section, we see how to integrate expressions like `int(dx)/((x^2+9)^(3//2))` depending on the function we need to integrate, we substitute one of the following trigonometric expressions to simplify the integration:.

You can evaluate the integral using integral calculator with steps easily online. Once the substitution is made the function can be simplified using basic trigonometric identities. Similarly, you can find double integral calculator on this website. Theorem if u = g(x) is a differentiable function whose range is an interval i and f is continuous on i, then ˆ f(g(x))g′(x)dx = ˆ f(u)du. This method of integration is helpful in …

Geneseo Math 222 01 Inverse Trig Functions from www.geneseo.edu

It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule backwards. Oct 19, 2021 · integration calculator with steps allows you to learn the concepts of calculating integrals without spending too much time. You can evaluate the integral using integral calculator with steps easily online. The first and most vital step is to be able to write our integral in this form: 164 chapter 8 techniques of integration z cosxdx = sinx+c z sec2 xdx = tanx+ c z secxtanxdx = secx+c z 1 1+ x2 dx = arctanx+ c z 1 √ 1− x2 dx = arcsinx+ c 8.1 substitution needless to say, most problems we encounter will not be so simple. Math ap®︎/college calculus ab integration and accumulation of change integrating using substitution. This method of integration is helpful in … By changing variables, integration can be simplified by using the substitutions x=a\sin(\theta), x=a\tan(\theta), or x=a\sec(\theta).

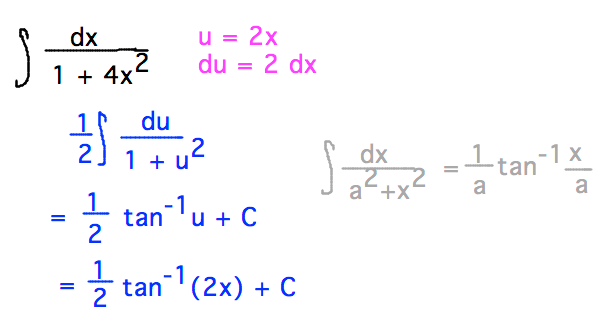
By changing variables, integration can be simplified by using the substitutions x=a\sin(\theta), x=a\tan(\theta), or x=a\sec(\theta).

This method of integration is helpful in … It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule backwards. Similarly, you can find double integral calculator on this website. Math ap®︎/college calculus ab integration and accumulation of change integrating using substitution. By changing variables, integration can be simplified by using the substitutions x=a\sin(\theta), x=a\tan(\theta), or x=a\sec(\theta). In this section, we see how to integrate expressions like `int(dx)/((x^2+9)^(3//2))` depending on the function we need to integrate, we substitute one of the following trigonometric expressions to simplify the integration:. This is the currently selected item. This has the effect of changing the variable and the integrand. The first and most vital step is to be able to write our integral in this form: Oct 19, 2021 · integration calculator with steps allows you to learn the concepts of calculating integrals without spending too much time. ∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand. The general form of integration by substitution is: You can evaluate the integral using integral calculator with steps easily online.

Once the substitution is made the function can be simplified using basic trigonometric identities. ∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand. Theorem if u = g(x) is a differentiable function whose range is an interval i and f is continuous on i, then ˆ f(g(x))g′(x)dx = ˆ f(u)du. Similarly, you can find double integral calculator on this website. 164 chapter 8 techniques of integration z cosxdx = sinx+c z sec2 xdx = tanx+ c z secxtanxdx = secx+c z 1 1+ x2 dx = arctanx+ c z 1 √ 1− x2 dx = arcsinx+ c 8.1 substitution needless to say, most problems we encounter will not be so simple.

Integration by trig substitution: x over square root of {4 from i.ytimg.com

The general form of integration by substitution is: Once the substitution is made the function can be simplified using basic trigonometric identities. Oct 19, 2021 · integration calculator with steps allows you to learn the concepts of calculating integrals without spending too much time. Theorem if u = g(x) is a differentiable function whose range is an interval i and f is continuous on i, then ˆ f(g(x))g′(x)dx = ˆ f(u)du. The first and most vital step is to be able to write our integral in this form: When dealing with definite integrals, the limits of integration can also change. You can evaluate the integral using integral calculator with steps easily online. ∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand.

164 chapter 8 techniques of integration z cosxdx = sinx+c z sec2 xdx = tanx+ c z secxtanxdx = secx+c z 1 1+ x2 dx = arctanx+ c z 1 √ 1− x2 dx = arcsinx+ c 8.1 substitution needless to say, most problems we encounter will not be so simple.

You can evaluate the integral using integral calculator with steps easily online. This is the currently selected item. Oct 19, 2021 · integration calculator with steps allows you to learn the concepts of calculating integrals without spending too much time. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule backwards. The first and most vital step is to be able to write our integral in this form: Once the substitution is made the function can be simplified using basic trigonometric identities. This method of integration is helpful in … Math ap®︎/college calculus ab integration and accumulation of change integrating using substitution. When dealing with definite integrals, the limits of integration can also change. 164 chapter 8 techniques of integration z cosxdx = sinx+c z sec2 xdx = tanx+ c z secxtanxdx = secx+c z 1 1+ x2 dx = arctanx+ c z 1 √ 1− x2 dx = arcsinx+ c 8.1 substitution needless to say, most problems we encounter will not be so simple. Similarly, you can find double integral calculator on this website. ∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand. In this section, we see how to integrate expressions like `int(dx)/((x^2+9)^(3//2))` depending on the function we need to integrate, we substitute one of the following trigonometric expressions to simplify the integration:.

This is the currently selected item. Once the substitution is made the function can be simplified using basic trigonometric identities. ∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule backwards. By changing variables, integration can be simplified by using the substitutions x=a\sin(\theta), x=a\tan(\theta), or x=a\sec(\theta).

INTEGRATION ALGEBRAIC FRACTIONS, integration from A-level from a-levelmathstutor.com

Math ap®︎/college calculus ab integration and accumulation of change integrating using substitution. Oct 19, 2021 · integration calculator with steps allows you to learn the concepts of calculating integrals without spending too much time. In this section, we see how to integrate expressions like `int(dx)/((x^2+9)^(3//2))` depending on the function we need to integrate, we substitute one of the following trigonometric expressions to simplify the integration:. Similarly, you can find double integral calculator on this website. ∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand. This is the currently selected item. Theorem if u = g(x) is a differentiable function whose range is an interval i and f is continuous on i, then ˆ f(g(x))g′(x)dx = ˆ f(u)du. When dealing with definite integrals, the limits of integration can also change.

Theorem if u = g(x) is a differentiable function whose range is an interval i and f is continuous on i, then ˆ f(g(x))g′(x)dx = ˆ f(u)du.

This has the effect of changing the variable and the integrand. Math ap®︎/college calculus ab integration and accumulation of change integrating using substitution. In this section, we see how to integrate expressions like `int(dx)/((x^2+9)^(3//2))` depending on the function we need to integrate, we substitute one of the following trigonometric expressions to simplify the integration:. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule backwards. This method of integration is helpful in … The first and most vital step is to be able to write our integral in this form: Theorem if u = g(x) is a differentiable function whose range is an interval i and f is continuous on i, then ˆ f(g(x))g′(x)dx = ˆ f(u)du. ∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand. Once the substitution is made the function can be simplified using basic trigonometric identities. You can evaluate the integral using integral calculator with steps easily online. 164 chapter 8 techniques of integration z cosxdx = sinx+c z sec2 xdx = tanx+ c z secxtanxdx = secx+c z 1 1+ x2 dx = arctanx+ c z 1 √ 1− x2 dx = arcsinx+ c 8.1 substitution needless to say, most problems we encounter will not be so simple. Similarly, you can find double integral calculator on this website. Oct 19, 2021 · integration calculator with steps allows you to learn the concepts of calculating integrals without spending too much time.

Integration By Substitution - Geneseo Math 222 01 Inverse Trig Functions / In this section, we see how to integrate expressions like `int(dx)/((x^2+9)^(3//2))` depending on the function we need to integrate, we substitute one of the following trigonometric expressions to simplify the integration:.. In this section, we see how to integrate expressions like `int(dx)/((x^2+9)^(3//2))` depending on the function we need to integrate, we substitute one of the following trigonometric expressions to simplify the integration:. This method of integration is helpful in … The first and most vital step is to be able to write our integral in this form: You can evaluate the integral using integral calculator with steps easily online. This has the effect of changing the variable and the integrand.

∫ f(g(x))g'(x)dx = f(t)dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand integration. The first and most vital step is to be able to write our integral in this form:

Source: a-levelmathstutor.com

You can evaluate the integral using integral calculator with steps easily online. The general form of integration by substitution is: Similarly, you can find double integral calculator on this website.

Source: www.math.canterbury.ac.nz

By changing variables, integration can be simplified by using the substitutions x=a\sin(\theta), x=a\tan(\theta), or x=a\sec(\theta). ∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand. In this section, we see how to integrate expressions like `int(dx)/((x^2+9)^(3//2))` depending on the function we need to integrate, we substitute one of the following trigonometric expressions to simplify the integration:.

Source: i.ytimg.com

When dealing with definite integrals, the limits of integration can also change. This is the currently selected item. 164 chapter 8 techniques of integration z cosxdx = sinx+c z sec2 xdx = tanx+ c z secxtanxdx = secx+c z 1 1+ x2 dx = arctanx+ c z 1 √ 1− x2 dx = arcsinx+ c 8.1 substitution needless to say, most problems we encounter will not be so simple.

Source: i.ytimg.com

The general form of integration by substitution is: This method of integration is helpful in … Math ap®︎/college calculus ab integration and accumulation of change integrating using substitution.

Source: i.ytimg.com

Math ap®︎/college calculus ab integration and accumulation of change integrating using substitution. Similarly, you can find double integral calculator on this website. Theorem if u = g(x) is a differentiable function whose range is an interval i and f is continuous on i, then ˆ f(g(x))g′(x)dx = ˆ f(u)du.

Source: i.ytimg.com

By changing variables, integration can be simplified by using the substitutions x=a\sin(\theta), x=a\tan(\theta), or x=a\sec(\theta).

Source: image2.slideserve.com

Theorem if u = g(x) is a differentiable function whose range is an interval i and f is continuous on i, then ˆ f(g(x))g′(x)dx = ˆ f(u)du.

Source: www.geneseo.edu

∫ f(g(x)).g'(x).dx = f(t).dt, where t = g(x) usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand.

Source: i.ytimg.com

Similarly, you can find double integral calculator on this website.

Source: a-levelmathstutor.com

The first and most vital step is to be able to write our integral in this form: